Can you train a neural network forever?
Understanding trainability in neural networks
One inauspicious day during my PhD, I ran an experiment. Following in the footsteps of Zhang et al., I tried training a neural network on a set of random labels of the MNIST dataset. It took a while, but eventually the network was able to fit the labels, getting 100% accuracy on this wholly contrived task.
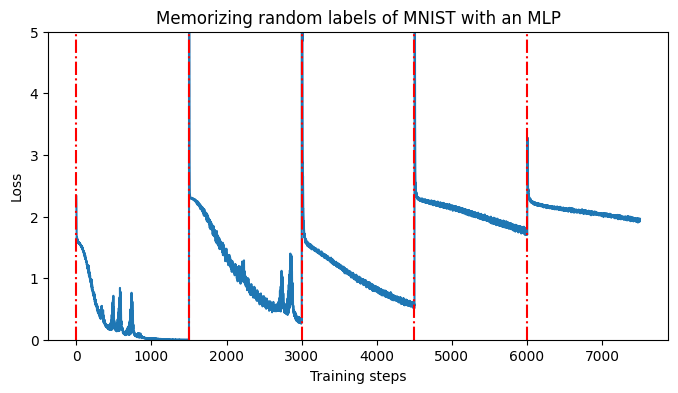 Memorizing a series of random labels results in progressively worse performance (red lines indicate label re-randomizations).
Memorizing a series of random labels results in progressively worse performance (red lines indicate label re-randomizations).
Then I went a little off-script.
I re-shuffled the labels and continued training. I repeated this process 20 times, fitting one set of random labels, then picking up from where the optimization process left off and fitting another set. And another. And another. Like Sysiphus, cursed to push a boulder up a mountain, day after day for eternity, my poor neural network was forced by heavy-ball momentum down a loss landscape, for as long as I set \(\texttt{iterations}\) in my code\(^1\). Unlike Sysiphus, however, my neural network was clearly not up to the task of repeating this process indefinitely. After a couple of random shuffles, my learning curves went from sharp drops to gentle inclines to plateaus as flat and vast as the Eurasian steppes. The network wasn’t learning anything.
Teaching old neural networks new tricks
I’d noticed this problem before, in a deep RL agent I trained on the video game Montezuma’s Revenge for an previous project. This is a domain where it is extremely difficult to achieve anything by taking random actions. The first set of points available to the player come from picking up a key, avoiding ghosts and pits, and using that key to open a door. Deep RL agents trained on this type of task typically run a very long time – on the order of millions of environment steps – without seeing any reward at all. Once they do see a reward, they have often so overfit to predicting a value of zero on every input that they are unable to respond to this new reward information and improve their behaviour. So this problem of a neural network becoming basically untrainable after training for a long time on some task wasn’t unheard of.
That said, montezuma’s revenge is very different from random label memorization. In sparse-reward reinforcement learning, the notion of overfitting I wanted to avoid was straightforward and predictable: if you ask a neural network to predict exactly zero, the best way to do so is to saturate the ReLU units so that no matter what weight value is assigned to them the output is precisely zero. But dead ReLU units are hard to propagate gradients through, so once the network is exposed to a non-zero prediction target it has no way to change its outputs.
In the case of the repeated label memorization tasks, something else had to be going on. At no point did I set as an optimization objective a problem whose solution involved saturating units in the network. The best way to minimize the cross-entropy loss with a set of labels is to assign high probability to each input’s assigned class. This requires having at least a few unsaturated units. Yet when I looked at the network internals, I was seeing dead ReLUs everywhere. I tried switching to a leaky ReLU activation, and while this stopped the catastrophic plateau issues I’d seen with ReLUs, it was hard to ignore the upward trend line in the loss as the number of training iterations ticked upward.
At this point, as a reasonably sane person who is probably more interested in developing AI for important applications like curing cancer or entertaining you while you do laundry than in contorting neural networks to solve absurd tasks like memorizing random labels of images, you’re probably thinking that I’m about to take you down an obscure and useless rabbit hole and are preparing to close this tab. It isn’t obvious that the pathologies neural networks fall prey to when repeatedly memorizing random bits of conflicting information, or when playing adversarially difficult video games, are at all analogous to the failure modes we encounter in large-scale training regimes. However, there is some evidence that they’re less dissimilar than you might think.
Trainability at scale
One issue known to plague LLMs is the phenomenon of “loss spikes”. In this case, a learning curve which had previously exhibited a reasonably consistent downward trajectory suddenly oscillates between high and low values, a behaviour that can destabilize training and even lead to divergence if you’re unlucky. This is a big problem if your training run costs millions (or at least hundreds of thousands) of dollars. The behaviour of neural networks around these loss spikes looks remarkably similar to what we see when we re-randomize a set of random labels. In the case of the random label memorization task, we observe that immediately after a task change, the second moment statistics used by an adaptive optimizer will be out of date, and specifically will underestimate the true gradient magnitude, because we have gone from perfectly fitting the old labels to making wildly inaccurate predictions on the new labels. As a result, the effective step size of the network is enormous. This effect, coupled with the fact that the best way to reduce the cross-entropy loss while a network is making confidently wrong predictions is to reduce the logit magnitude, and hence also the output magnitude of many hidden units, results in sudden drops in the pre-activation values of many units, which in extreme cases results in unit death.
Since both pathologies exhibit similar underlying mechanisms it turns out that they can be solved by similar strategies. A simple solution is to set the \(\epsilon\) value in the denominaor of the Adam update rule to a larger value, so that the effective step size is bounded, and to set the EMA parameter of the second moment estimates to update faster. This is the approach we found worked well in a paper presented at ICML this year. This is also the approach that other folks found worked well in a paper presented at NeurIPS last week to reduce the prevalence of loss spikes in large language models.
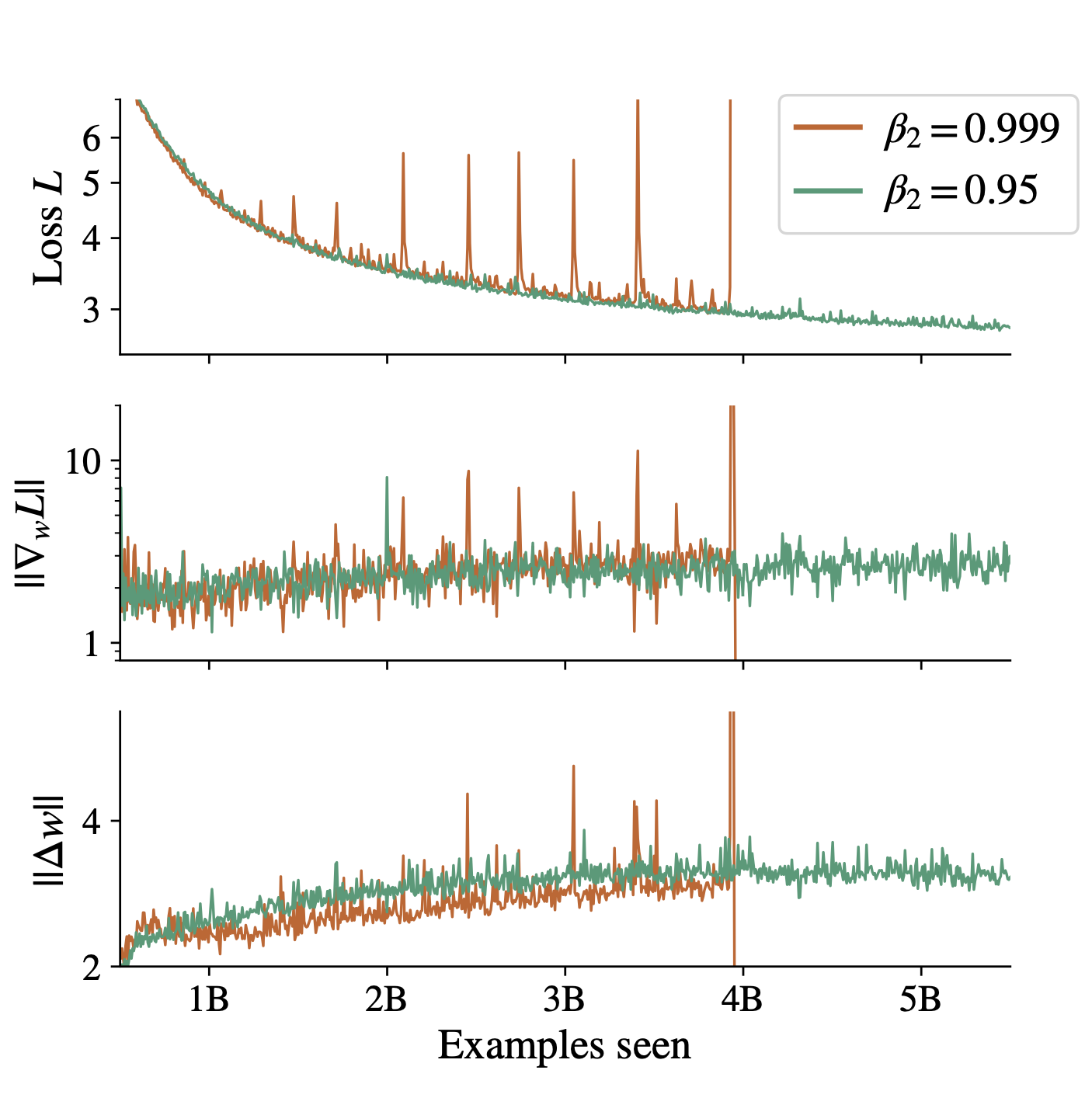
So there is at least one example where this type of experiment ends up producing a solution that can also be adopted in training large models. In fact, even if you’re not at all interested in training large models, designing learning algorithms that are robust to nonstationarity is critically important to another domain which, at least in the past, also captured the public imagination: reinforcement learning. Another relevant paper at NeurIPS this year observed that simply resetting the optimizer every time the target network is reset in a deep RL agent. In this case, since you know exactly when the first- and second-moment gradient estimates will become inaccurate, you can just reset them at that moment, rather than having to tune your \(\beta_2\) parameter by trial and error. Indeed, the whole reason why I started looking into random label memorization was because I wanted to figure out why it was so hard to get good performance out of an RL agent without extensive hyperparameter tuning.
Trainability in reinforcement learning
Over the past couple of years, it has become obvious that part of the reason why it is so hard to train deep RL agents has less to do with the intricacies of reinforcement learning – resolving issues like de-biasing Bellman backups, tuning importance sampling ratios, and navigating the bias-variance tradeoff of N-step returns – and more to do with basic neural network training than had perhaps been previously thought. In other words, it’s not that the signal we are giving the networks is bad, it’s that the networks wouldn’t even be able to use that signal to improve their performance if it were perfect. A network trained on a deep RL task runs into the peculiar problem of becoming less trainable the more you train it.
Networks become less trainable over time in deep RL
What exactly do I mean by less trainable? Well, I mean a couple of things. First, I mean that if you try to train it on something completely new for some fixed optimizer budget, the final training loss you get on the new thing will be worse than if you’d started from its freshly initialized parameters. Second, I mean that even if you train long enough that you can get epsilon train loss, you will still have a network that generalizes worse (assuming there is structure to be generalized) than the one that started from a random initialization. There are a few related phenomena under this umbrella which have been observed in the literature.
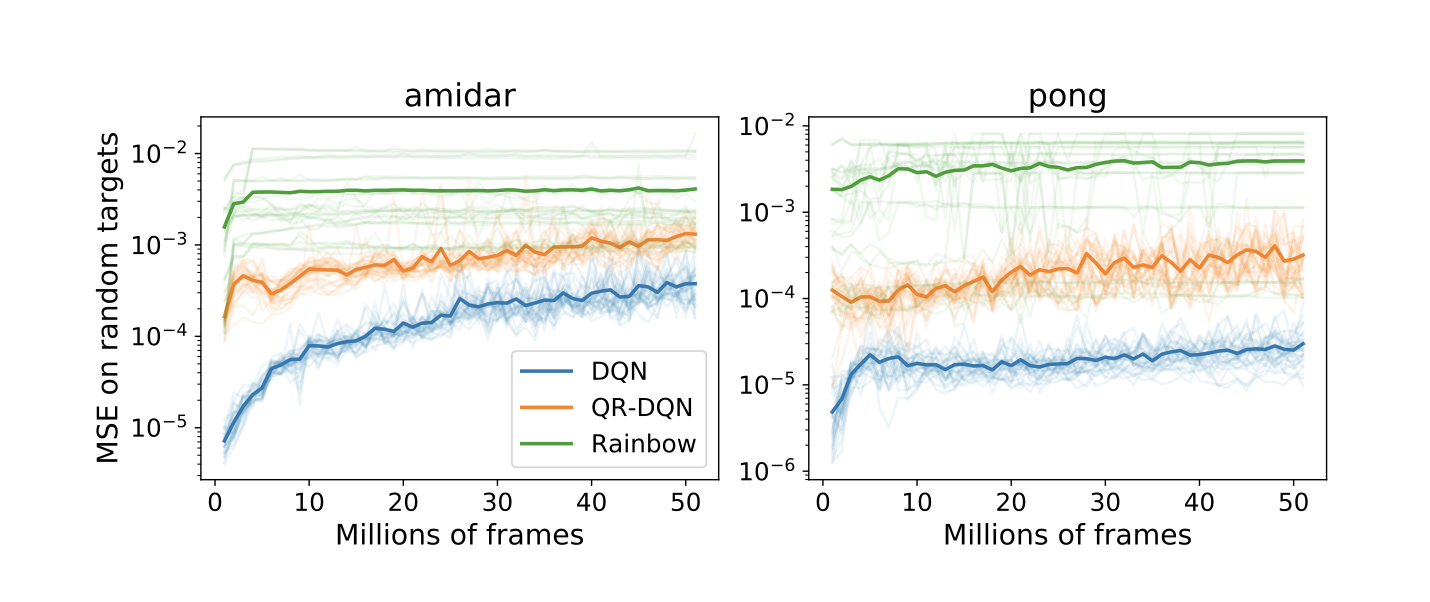 Training a network in deep RL tasks tends to make it worse at fitting new targets (from this paper).
Training a network in deep RL tasks tends to make it worse at fitting new targets (from this paper).
Capacity loss: neural networks get worse at learning new things unrelated to their primary task when trained with value-based deep RL methods. The main experiment I think of in this paper trains a neural network on a game from the Atari benchmark, then takes network checkpoints from different stages of the training trajectory and trains them on a new regression task (akin to memorizing random noise). Later checkpoints invariably do worse on this new task than earlier ones.
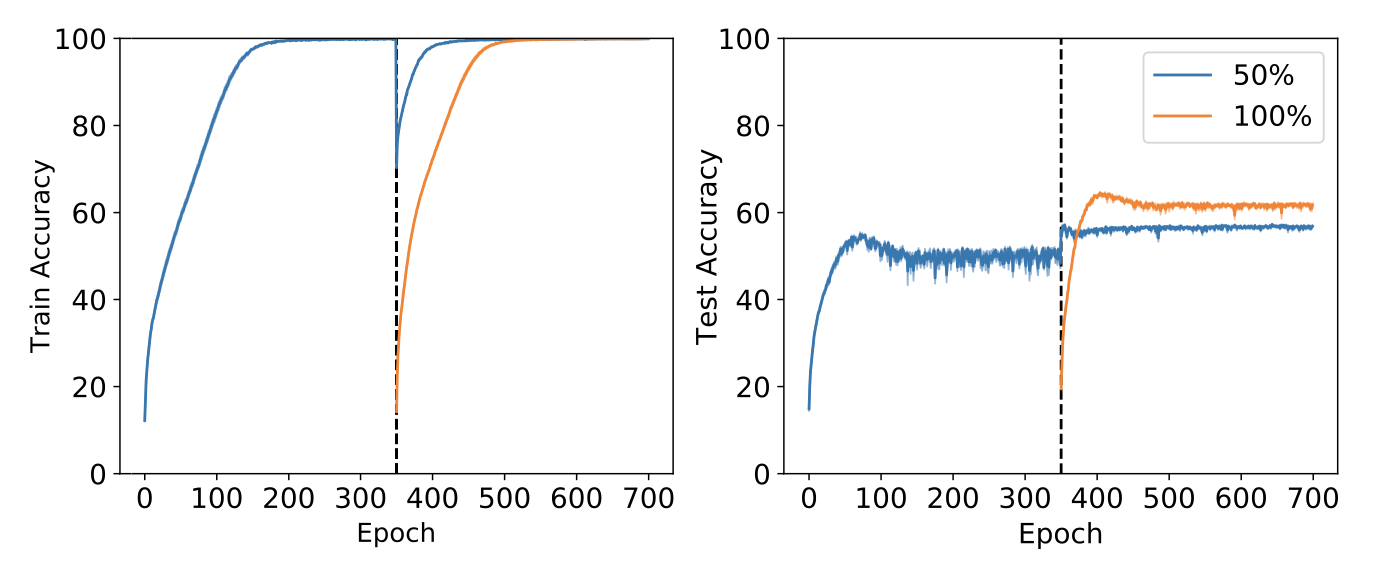 Pretraining on half of CIFAR-10 then training on the whole dataset hurts generalization (Ash & Adams, 2020)..
Pretraining on half of CIFAR-10 then training on the whole dataset hurts generalization (Ash & Adams, 2020)..
Warm-starting: overfitting on a small subset of data can permanently inhibit the ability of a network to learn features that generalize over the whole dataset. The experiment encapsulating this effect trains a neural network on half of the CIFAR-10 dataset (which half doesn’t seem to particularly matter) until it attains zero train error, then adds in the second half and trains until the network gets zero error on the whole dataset. The resulting generalization performance is about 10 percentage points lower than what you would get by training on the whole dataset from scratch.
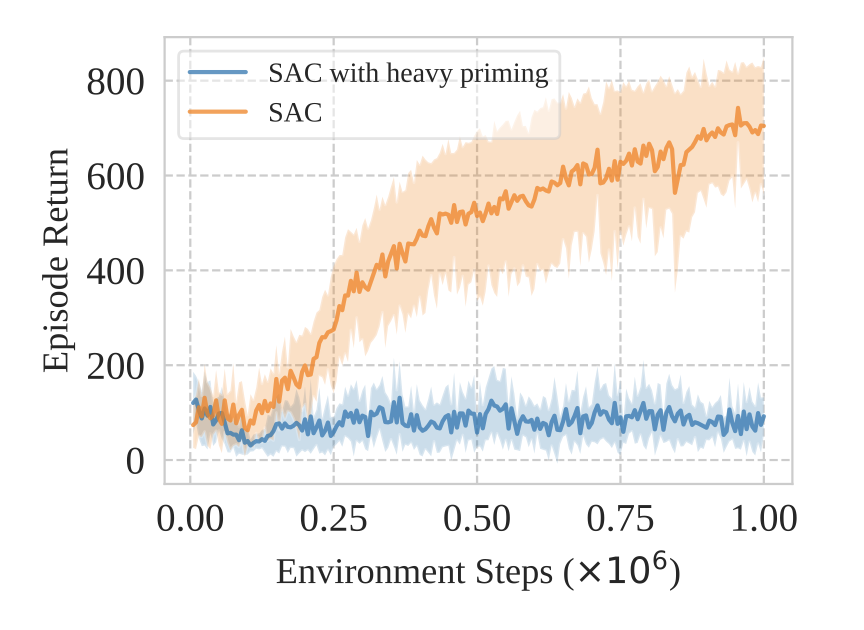
Primacy bias: networks trained in deep RL overfit to their early data in a way that reduces their ability to improve their performance later (although it is unclear whether this is due to an inability to reduce the training loss or the generalization gap, in whatever sense it is valid to talk about these things in the RL context). This can be exacerbated by training for many optimizer updates per environment step, giving the agent more of a chance to overfit on early data. In extreme cases, this prevents the agent from learning at all (see adjacent figure for an example).
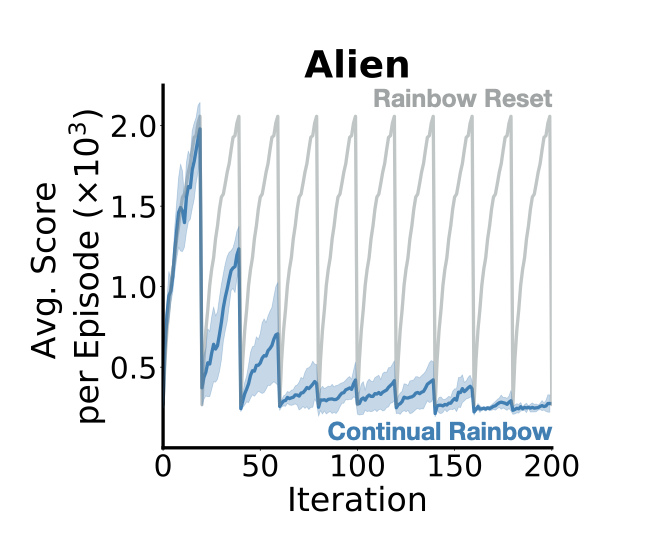
Plasticity: this is an umbrella term for a variety of phenomena related to the ability of a network to learn new things. It tends to be used in the context of evaluations that look at a network’s ability to increase a performance measure on some RL task, although it also appears in the continual learning literature. This choice of terminology is popular among people who live in or have been to Edmonton. A lot of papers discussing loss of plasticity, particularly in deep RL, look at the robustness of the learning algorithm to some sort of change in the task, for example switching between Atari environments or adding some particular kind of nonstationarity into the task.
Why do neural networks lose plasticity?
There is an old saying in the deep learning literature, which goes something like this:
“Trainable networks are all alike; every untrainable network is untrainable in its own way.” - Unknown.
There are very few ways for a network to be trainable. Gradients cannot explode or vanish; features cannot become degenerate, nor can they splinter into disjoint pieces; updates must generalize between inputs, but not too much. A freshly initialized neural network is balanced on a knife’s edge between chaos and collapse. It is no wonder that, as they train, neural networks often lose the very properties that made them trainable in the first place. A neural network is a highly dynamic object during training – this dynamism is how learning happens. But this also poses a challenge for developing robust learning algorithms, as it is difficult to pin down which of the myriad changes in the network is driving plasticity loss. One might hope that loss of plasticity is being driven by changes in a few easy-to-compute statistics, which can then be explicitly regularized. But it is not at all obvious a priori whether this is the case.
Indeed, this was something that I investigated about a year ago for a paper which had the lofty goal of understanding plasticity in neural networks. A number of network properties had been demonstrated to correlate with plasticity loss, and so it was a natural question to ask whether these properties might be promising causal mechanisms. I looked at a few of these: parameter norm, weight rank, feature rank, and the number of dead units in the network. I trained a few networks on a simple RL task and then, at various points in the RL training loop, copied the parameters and used them as an initialization to fit an unrelated regression task. This gave a rough sense of how plasticity was evolving over time and across networks, of which there were many as I varied the optimizer, observation space, reward function, and network architecture to generate a variety of experimental settings. I then asked the question: is the direction of the correlation between each of these quantities and plasticity consistent across experimental settings? If parameter norm was driving plasticity loss, for example, we would expect that networks with larger parameter norms would always be less plastic than ones with smaller norms, independent of the dataset you trained them on. Somewhat surprisingly, we observed that this was not the case; none of the statistics we looked at were robust predictors of plasticity.
The model that has emerged instead is one where a few main drivers interact to cause plasticity loss in neural networks. While none can be blamed for plasticity loss in all cases, taken in conjunction they explain most of the issues I’ve encountered where the network cannot reduce its training loss (generalization issues are another matter entirely). The issues are pretty straightforward: unbounded parameter norm growth causes numerical issues, pathological sharpness, and reduced effective step size of the optimizer, saturated activations results in a less expressive network in which some units are unable to effectively propagate gradients and is compounded by feature drift, and finally output scaling as a result of fitting unnormalized targets produces ill-conditioned loss landscapes. Tricks like layer normalization and weight decay, as I’ll discuss more in the next section, can go a long ways towards addressing these issues and, provided you use a large enough network, result in networks that can be trained on highly adversarial nonstationary data distributions with no apparent reduction in performance.
Of course, just because a network is trainable doesn’t mean that the generalization gap it reaches after minimizing the training loss will be commensurately low. Indeed, it stands to reason that a lot of the benefits we see from resets, particularly in deep RL, are likely due to avoiding overfitting rather than to improved training dynamics. One point supporting this was a recent ICLR submission I spotted while doing lit review for this post, where they found that in mujoco-style domains resets end up producing a suspiciously similar effect on training curves as data augmentation, and also doesn’t provide any benefits when used in conjunction with data augmentation.
How do you solve a problem like trainability?
There are a variety of ways one can try to avoid the problem of networks losing plasticity. Most approaches in the literature cluster around a few main ideas:
Reset the network
Reset some layers in the network
Reset problematic neurons in the network
Reset all the parameters, but not all the way
Regularize the network parameters or features to avoid divergence
Constrain the network parameters and features to maintain first/second moments targeted by most initializations
Resets
Resets are a shockingly common trick across deep RL. The more nonstationary the domain, the more likely it is that at some point the researchers tried turning their agent off and on again. Resets turn up in multiagent settings (e.g. the capture the flag paper from 2019 and the AlphaStar paper<). They turn up in large-scale regimes (e.g. AdA and BBF). They turn up in multitask problems (e.g. kickstarting). Wherever you look, someone has tried to turn their agent off and on again and found that it solved their problem.
But resets aren’t ideal in a lot of ways. When you reset a network, you’re forcing it to erase all of the useful previous knowledge it had accumulated over the course of its “life” so far, which means you then have to get it back up to speed, and quickly, afterwards. In deep RL, the trick to doing this is to either distill on the network’s old outputs, or to train on the previous network’s experiences. Distillation is a lot faster than training from scratch, but it still means that a nontrivial chunk of your training budget is spent on your agent teaching itself things it already knows.
Despite being inefficient, resets are far from ineffective. For the same compute budget, kickstarted networks often significantly outperform counterparts that don’t use resets. When this happens, the original agent usually hits a plateau that it cannot overcome, while the reset agent blows past this performance level and sees dramatically higher scores on the task.
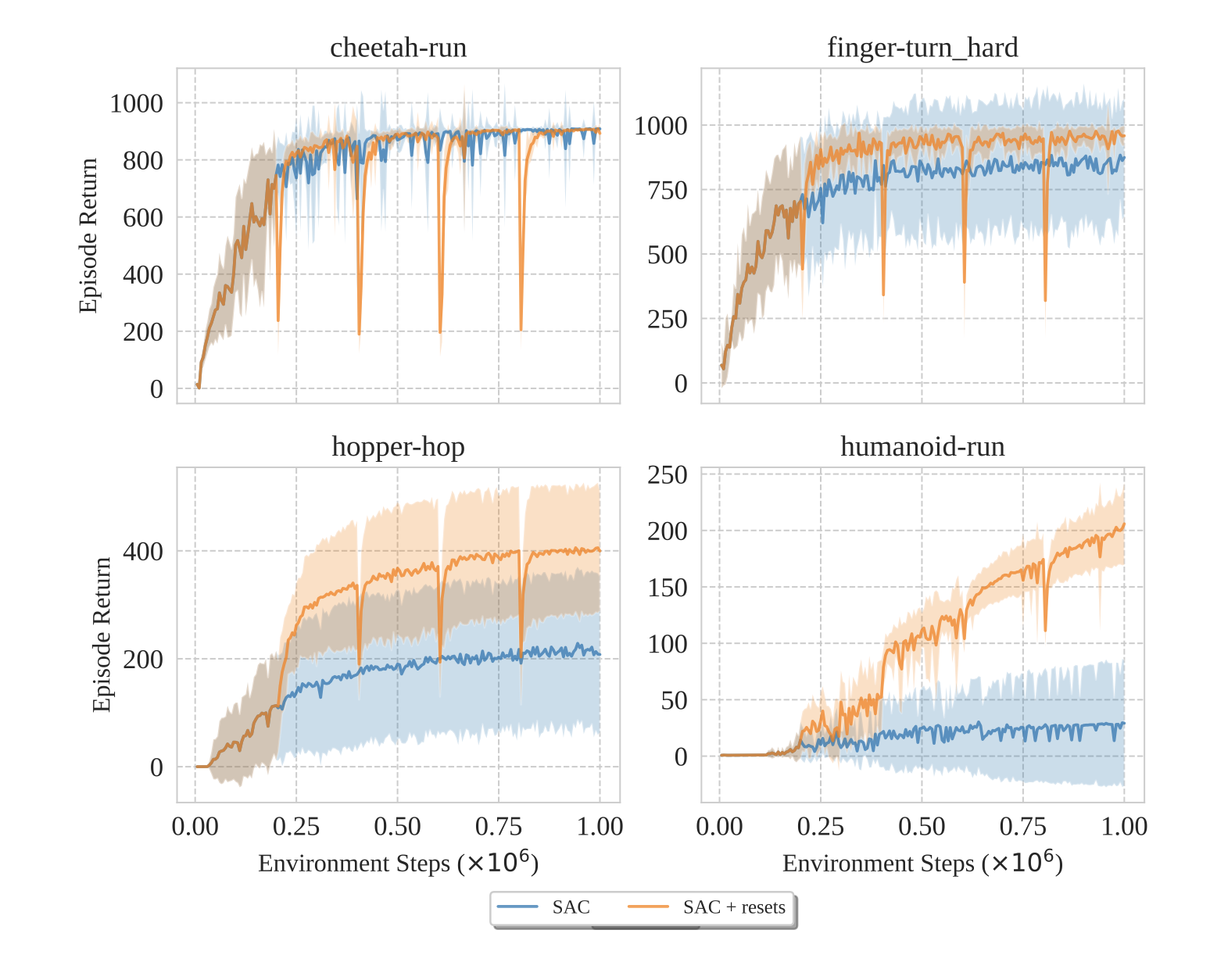 Resets can break through plateaus (Nikishin et al.)
Resets can break through plateaus (Nikishin et al.)
In some cases, it is possible to avoid resetting the whole network and instead reset problematic components. This can significantly speed up learning, especially if the resets are done in such a way that minimally influences the agent’s policy. For example, Sokar et al. only reset individual ReLU units once they have saturated (and do so in such a way that the network’s output doesn’t change), and Nikishin et al. only reset the last few layers of the network, observing that resetting the earlier layers slows down retraining without adding additional performance benefits. Another strategy involves doing a softer form of reset called “shrink and perturb” where the weights are scaled by some \(\beta < 1\) and then perturbed by a random initialization. This is the strategy used by a number of recent works as it still biases the network towards a good set of parameters, but it also adds enough randomness that it lets the network escape bad ‘local minima’\(^2\). This was the approach used by Ash and Adams when they were studying warm-starting in supervised learning problems. The approach makes a lot more sense in classification, where the argmax logit is scale-invariant and rescaling your parameters doesn’t change the decision function, compared to regression, where rescaling your parameters significantly changes your loss, but shrink and perturb still seems to help in deep RL domains.
The success of shrink and perturb, a method designed to improve generalization in deep RL highlights an important property of the reinforcement learning problem that is less salient in supervised learning: due to the nonstationarity in the input distribution, generalization and training performance are tightly intertwined. Whereas in supervised learning we can reason about our ability to drive down the training loss and then consider whether the function we found generalizes to new data, in deep RL an agent is constantly seeing new data during the training process, and so generalizing correctly is crucial to its ability to quickly improve its performance. This means that it is extremely difficult to disentangle the effect of resets on the ability of a deep RL agent to overwrite spurious features and the effect of resets on the ability of a deep RL agent to reduce its temporal difference error on transitions it has already seen if all we are looking at is raw performance. There’s also the problem of trying to use resets for supervised learning problems where getting the network back up to speed will encounter precisely the same pitfalls as were encountered in training it in the first place. So if resets aren’t (always) the answer, what else can we look to as a possible solution?
Regularization
Neural network initializers have been tuned for a long time to make networks highly trainable. Optimizers, in contrast, have not been optimized (pun not intentional) to maintain this property. In most machine learning problems people have historically studied, this wasn’t an issue. The longer a neural network trains on a fixed learning problem, the better its performance gets and the less remains for it to learn. It is only in non-stationary problems like RL, or in extremely large and difficult datasets where training runs last so long that the rate of plasticity loss exceeds the rate of progress on the problem, that this mismatch becomes apparent. This observation leads to a natural question: is it possible to tweak optimization algorithms in such a way that you don’t slow down training, but still manage to improve the stability and generalization of the network?
The oldest trick in the book is weight decay; this strategy obviously makes a lot of sense if the thing making your network untrainable is that the parameter norm has grown too big. There are a couple of ways that this could happen: the most straightforward one is that large parameters tend to produce large gradients and Hessians, which increases the loss landscape sharpness and makes optimization more difficult, especially if you are using a method like adam or rmsprop which tries to perform fixed-norm updates. Another issue can come up if you use normalization layers, where the effective optimizer step size shrinks as the input feature norm grows. In this sense, keeping the parameter norm small stabilizes learning – it also tends to make the optimization process much less likely to kill off or saturate units, since the small weight norm tends to reign in diverging preactivations.
There are a couple of other examples of this strategy, especially in deep RL. One trick that I tried – which mostly was designed to avoid features from completely collapsing – was to regularize layer outputs towards their values at initialization. Another approach that Agarwal et al. tried was to regularize the rank of the features, or to explicitly avoid issues that arise from using the bootstrapping operator in offline RL. I’ve also seen strategies that involve regularizing the network parameters towards their initial values, and regularizing the distribution over parameters towards the empirical distribution at initialization. The main problem with regularization approaches is that the weight on the regularization term has to be carefully tuned to achieve the desired effect: too small of a penalty and the regularized quantity might still grow unboundedly; too large and convergence slows down on the primary task of interest.
Constraining the optimization trajectory
Rather than trying to precisely tune the multiplier used on a regularization term, we can explicitly constrain the quantity we’re interested in preserving. This has two main benefits: first, we don’t have to worry about whether the property we’re interested in is changing over the course of training; second, we know that if the constraint improves performance, it was because of preserving the target property, rather than some other ancillary effect of the regularizer. This doesn’t work for all quantities we might want to regularize, since it isn’t always the case that there’s a straightforward way of projecting a parameter vector onto the set of parameterizations which preserve the property we want to constrain, but when it is possible this is often a much easier route to go than regularization. For example, we could try to penalize the feature norm, but an easier and more effective strategy is to simply normalize the features directly via layernorm. Similarly, we could apply weight decay to the network, or we could normalize the weights to maintain the norm they had at initialization.
Empirically, normalization – especially layer norm – is extremely effective at improving optimization dynamics on a single task and also providing greater robustness to nonstationarities. The difference between an unconstrained and a constrained network can be night and day when looking at particularly pernicious nonstationarities, like memorizing sequences of random labels of an image dataset, but even in deep RL there can be dramatic performance improvements from just applying layer normalization. I don’t think I’ve encountered an agent which didn’t benefit from layer normalization on the arcade learning environment benchmark, for example. Further, many approaches to improve the stability of large language models such as QK-norm work by adding more normalization layers into pieces of the network that had previously been overlooked.
Constraining the norms of features and weights isn’t all sunshine and rainbows, however. In some cases, adding in these constraints does reduce the expressive power of the network, which means that the improved robustness that you see comes at the cost of reduced performance on a single task. I’ve found that this can be overcome by increasing the width of the network, but buyer beware: if you stop the network from going into weird regions of parameter space with bad properties, you may also prevent it from reaching niche regions of parameter space with good properties too.
Concluding remarks
I’ve tried to fit a lot of information into this post, so it’s worth recapping the important pieces.
- There are a lot of settings where neural networks can be shown to become less trainable over time.
- Resetting the network can recover trainability in some cases, but not all. It also has other benefits on generalization and learning dynamics that are harder to characterize.
- Constraining the network to have the properties that initializations are designed to promote, such as constant per-layer gradient and feature norms, is a surprisingly effective way to maintain trainability, and is a lot easier to tune than equivalent regularization strategies.
One of the big open questions that remains in this area concerns overfitting and interference between distributions over time. Resetting strategies like shrink-and-perturb, kickstarting seem to be the best solution we’ve found so far, but there’s something aesthetically displeasing to me about the idea of constantly having to completely reset the network periodically during training. This approach also won’t fix problems that crop up in extremely long training runs, where the process of distilling prior knowledge from the previous trained parameters is as difficult as learning that knowledge in the first place. In the long run, we would like a way for neural networks to gracefully incorporate new information and learn to generalize across data seen over time. Today that future looks a long way off, but I hope to see exciting developments towards it in 2024 and beyond.
Footnotes
1. There are many resources for PhD students struggling with their mental health. I personally believe that an under-appreciated strategy for deep learning PhDs is to analogize themselves to Greek gods as frequently as their schedule allows. There is something empowering in the thought that you are to neural networks what Greek deities were to mortal men at times when Reviewer 2 is calling your paper a waste of bandwidth to host on arxiv.
2. I don’t really mean local minima in the strict sense here, but rather loss landscape regions that resemble the Canadian Prairies in their flatness and lack of interesting features, and from which it is very difficult to get out via gradient descent.